Using the expanded accounting equation solve for the missing amount – Using the expanded accounting equation to solve for missing amounts is a fundamental technique in accounting that enables the determination of unknown financial data. This comprehensive guide delves into the concept, applications, and limitations of this valuable tool, providing a clear understanding of its significance in financial analysis.
The expanded accounting equation, expressed as Assets = Liabilities + Owner’s Equity, serves as the foundation for understanding the financial position of an entity. By manipulating this equation, accountants can isolate and solve for missing amounts, such as assets, liabilities, or equity, when only partial financial information is available.
1. Expanded Accounting Equation Overview

The expanded accounting equation, also known as the balance sheet equation, is a fundamental accounting principle that states that the total assets of a business must equal the sum of its liabilities and owner’s equity. This equation can be expressed as:
Assets = Liabilities + Owner’s Equity
The expanded accounting equation is a useful tool for understanding the financial health of a business and can be used to analyze financial data, solve for missing amounts, and make informed decisions.
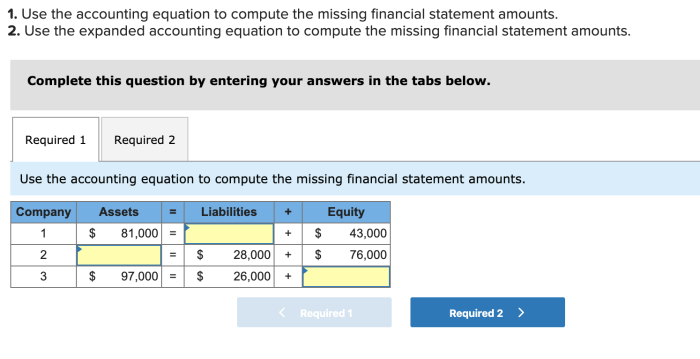
2. Solving for Missing Amounts
The expanded accounting equation can be used to solve for missing amounts in financial statements. To do this, simply rearrange the equation to solve for the unknown variable. For example, if you know the total assets and liabilities of a business, you can solve for owner’s equity by subtracting liabilities from assets:
Owner’s Equity = Assets
Liabilities
The following table shows an example of how to solve for missing amounts using the expanded accounting equation:
| Account | Amount |
|---|---|
| Assets | $100,000 |
| Liabilities | ? |
| Owner’s Equity | $20,000 |
To solve for liabilities, we can rearrange the equation to:
Liabilities = Assets
Owner’s Equity
And then plug in the known values:
Liabilities = $100,000
$20,000 = $80,000
3. Applications of Solving for Missing Amounts: Using The Expanded Accounting Equation Solve For The Missing Amount

Solving for missing amounts using the expanded accounting equation is essential in a variety of real-world scenarios. For example, businesses use this equation to:
- Analyze financial statements
- Prepare budgets
- Make investment decisions
- Identify financial trends
By understanding how to solve for missing amounts, businesses can gain a better understanding of their financial position and make more informed decisions.
4. Limitations and Considerations
While the expanded accounting equation is a useful tool, it is important to be aware of its limitations. One limitation is that the equation only provides a snapshot of a business’s financial health at a specific point in time. Additionally, the accuracy of the results obtained from solving for missing amounts depends on the accuracy of the data used.
When using the expanded accounting equation, it is also important to consider the following factors:
- The type of business
- The industry in which the business operates
- The accounting principles used by the business
5. Advanced Techniques
In some cases, it may be necessary to use advanced techniques to solve for missing amounts. These techniques include:
- Using matrices
- Using linear programming
- Using other mathematical methods
These techniques can be used to solve complex missing amount problems that cannot be solved using the basic steps Artikeld above.
Common Queries
What are the steps involved in solving for missing amounts using the expanded accounting equation?
The steps involve identifying the missing amount, rearranging the equation to isolate the unknown variable, and performing the necessary calculations.
What are some real-world applications of solving for missing amounts?
Examples include calculating depreciation expenses, determining inventory values, and analyzing financial ratios.
What are the limitations of using the expanded accounting equation to solve for missing amounts?
Limitations include the potential for estimation errors, reliance on accurate financial data, and the inability to account for complex transactions.