Identify the segment bisector of jk – Identifying the segment bisector of JK is a fundamental concept in geometry, providing a precise method for dividing a line segment into two equal parts. This comprehensive guide will delve into the definition, methods, properties, and applications of segment bisectors, empowering readers with a thorough understanding of this essential geometric concept.

Understanding the concept of segment bisectors is crucial for students of geometry, as it forms the basis for solving various geometric problems. It is also widely used in architecture, engineering, and other fields where precise measurements and constructions are essential.

Segment Bisector of JK

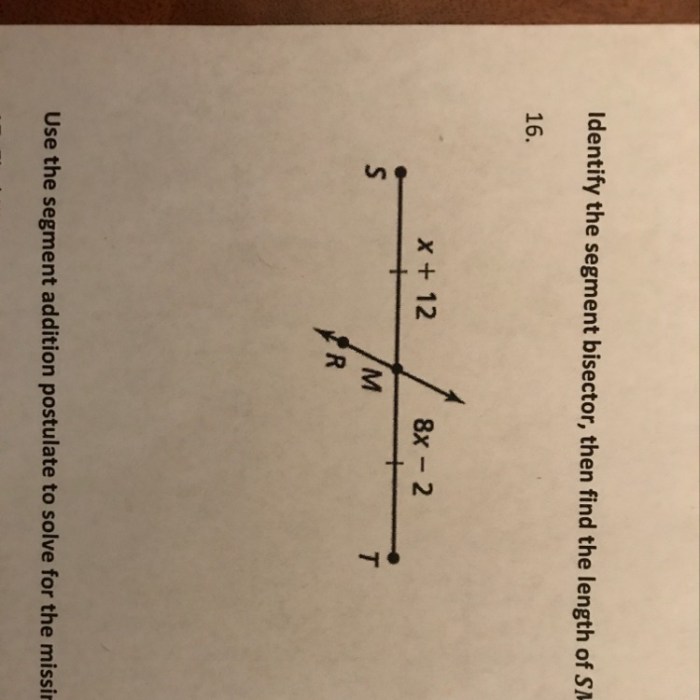
A segment bisector is a line or ray that passes through the midpoint of a line segment and divides it into two equal parts. It is perpendicular to the line segment and intersects it at its midpoint.

Illustration

Consider line segment JK. Its segment bisector, LM, passes through the midpoint, M, of JKand is perpendicular to JKat M.

Identifying the Segment Bisector

The segment bisector of a line segment is a line, ray, or line segment that divides the segment into two equal parts. There are several methods for identifying the segment bisector of a line segment JK.

Using a Compass and Ruler

This method involves using a compass and a ruler to construct the segment bisector.

1. Place the compass point at one endpoint of the line segment, say J.
2. Set the compass width to be greater than half the length of the line segment.
3. Draw two arcs that intersect the line segment on either side of J.
4. Repeat steps 1-3 with the compass point at the other endpoint, K.
5. The two arcs will intersect at a point M on the line segment.
6. The line segment JM is the segment bisector of JK.

Using Geometric Properties

The segment bisector of a line segment has several geometric properties that can be used to identify it.

• Distance from Endpoints:The segment bisector is equidistant from the endpoints of the line segment.
• Perpendicular Bisector:The segment bisector is perpendicular to the line segment and passes through its midpoint.
• Angle Bisector:The segment bisector bisects the angle formed by the line segment and a line parallel to it.

Properties of the Segment Bisector

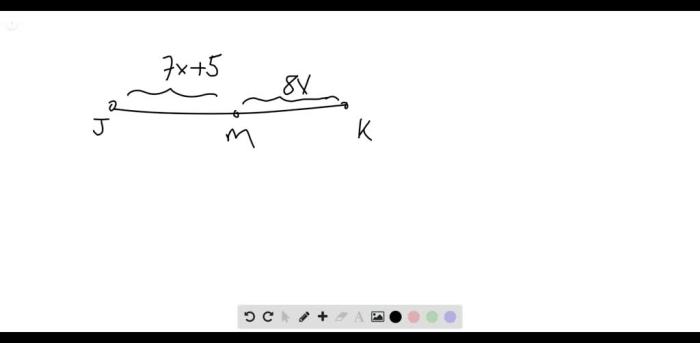
The segment bisector of a line segment is a unique line or ray that divides the segment into two congruent parts. It is perpendicular to the segment at its midpoint.

Congruent Parts

The segment bisector divides the segment into two congruent parts. This means that the lengths of the two segments created by the bisector are equal. This property is essential for ensuring that the segment is divided equally.

Relationship to Midpoint

The segment bisector passes through the midpoint of the segment. The midpoint is the point that divides the segment into two equal parts. The segment bisector is perpendicular to the segment at the midpoint, forming a right angle. This relationship ensures that the segment is divided into two congruent parts and that the bisector is perpendicular to the segment.

Applications of Segment Bisectors: Identify The Segment Bisector Of Jk

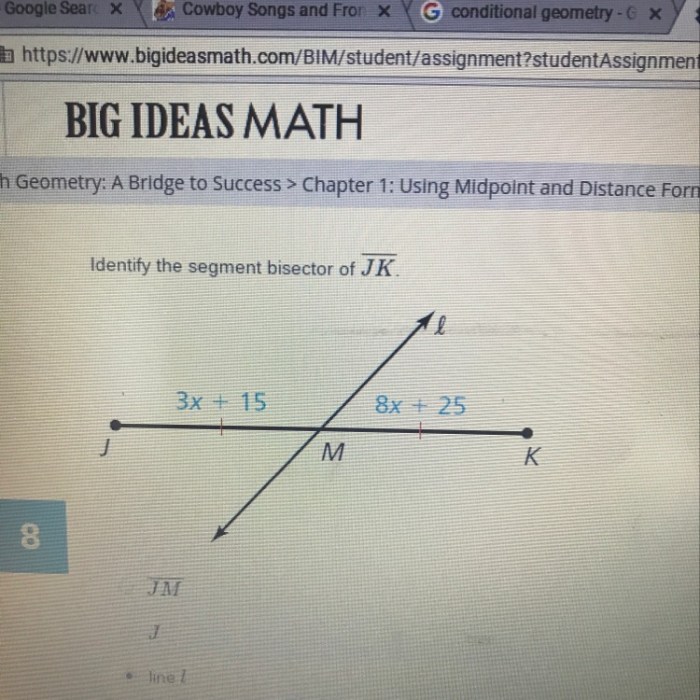
Segment bisectors are valuable tools in geometry and have practical applications in various fields. They are used to determine the midpoint of a segment, divide an angle into two equal parts, and construct perpendicular bisectors to create circles and other geometric shapes.

Applications in Geometry

In geometry, segment bisectors play a crucial role in:

• Finding the midpoint of a segment: A segment bisector intersects the segment at its midpoint, dividing it into two equal parts.
• Constructing perpendicular bisectors: A perpendicular bisector of a segment is a line that passes through the midpoint and is perpendicular to the segment. It divides the segment into two congruent right triangles.
• Creating circles: A circle can be constructed by using the perpendicular bisector of a segment as the radius and the midpoint as the center.
• Solving angle bisector theorems: The angle bisector theorem states that the ratio of the lengths of the segments created by an angle bisector is equal to the ratio of the lengths of the opposite sides of the triangle.

Applications in Other Fields

Segment bisectors also have applications in:

• Architecture and design: Segment bisectors are used to create symmetrical designs and ensure balance in structures.
• Engineering: Segment bisectors are used to determine the center of mass and the moments of inertia of objects.

li>Navigation: Segment bisectors can be used to find the midpoint of a line segment representing a path, helping to determine the optimal route.

• Computer graphics: Segment bisectors are used in computer graphics algorithms for line drawing, shape manipulation, and image processing.

Variations and Extensions

The concept of segment bisectors extends beyond its basic definition and application. Variations of segment bisectors, such as angle bisectors, provide valuable insights into geometric constructions and relationships.

In higher dimensions, the concept of segment bisectors can be generalized to hyperplanes and subspaces. For instance, in three-dimensional space, the perpendicular bisector of a line segment becomes a plane that divides the space into two equal halves.

Angle Bisectors

Angle bisectors are closely related to segment bisectors. An angle bisector is a line that divides an angle into two equal parts. The intersection point of the angle bisectors of a triangle is known as the incenter, which is equidistant from the three vertices of the triangle.

Higher Dimensions, Identify the segment bisector of jk

In higher dimensions, the concept of segment bisectors can be extended to hyperplanes and subspaces. For example, in four-dimensional space, the perpendicular bisector of a line segment becomes a three-dimensional hyperplane that divides the space into two equal halves.

Open Questions and Research Areas

Several open questions and areas for further research exist related to segment bisectors. One area of exploration is the relationship between segment bisectors and other geometric constructions, such as perpendicular bisectors and angle bisectors.

Questions and Answers

What is the definition of a segment bisector?

A segment bisector is a line, ray, or line segment that divides a given line segment into two congruent parts.

How do you identify the segment bisector of JK?

There are several methods to identify the segment bisector of JK, including using a compass and straightedge, constructing perpendicular bisectors, or using analytic geometry.

What are the properties of a segment bisector?

Segment bisectors have several unique properties, including being perpendicular to the line segment at its midpoint, dividing the line segment into two congruent parts, and being the locus of points equidistant from the endpoints of the line segment.